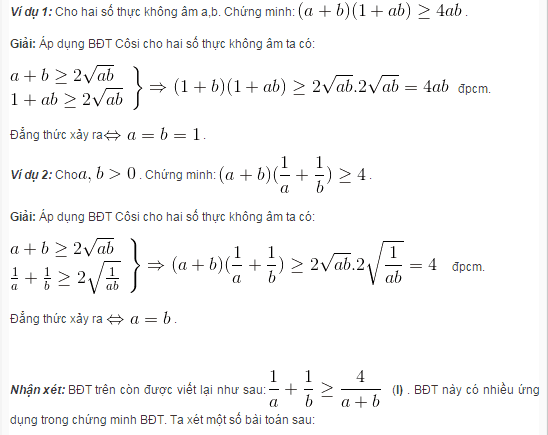Bất đẳng thức cosi là gì và những điều cần biết

Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức cosi. Vậy bất đẳng thức cosi là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!

Bất đẳng thức cosi là gì?

Bất đẳng thức Cosi có thể được phát biểu một cách khái quát như sau:

Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng. Trường hợp trung bình cộng và trung bình nhân của chúng chỉ bằng nhau khi n bằng nhau.

Phát biểu này có thể được trình bày như sau:

Với 2 số thực a và b (a, b > 0, R), ta có:

a + b2ab

Dấu “=” xảy ra a=b

Bất đẳng thức này cũng áp dụng với n số thực dương:

x1 + x2 + … + xnnnx1.x2…..xn (n>1, N)

Dấu “=” xảy ra x1=x2=…=xn

Chứng minh bất đẳng thức cosi

Chứng minh bất đẳng thức với 2 số thực a, b không âm

Ta thấy với a = 0 hoặc b = 0 thì ta thấy bất đẳng thức luôn đúng. Vì vậy chúng ta chỉ chứng minh bất đẳng thức Cosi với 2 số dương mà thôi:

ab2 ≥ ab

<=>

ab≥2ab

<=>

a−2abb≥0

<=>

(a−b)2≥0

( vì a, b >0) luôn đúng

=> Bất đẳng thức đã cho luôn đúng với ∀ a, b dương (đpcm)

Chứng minh bất đẳng thức với 3 số thực a, b, c không âm

Với a = 0 hoặc b = 0 hoặc c= 0 thì bất đẳng thức luôn đúng. Vì thế chúng ta cũng chỉ chứng minh bất đẳng thức với 3 số dương mà thôi

Chứng minh bất đẳng thức với 4 số thực a, b, c, d không âm

Với a = 0 hoặc b = 0 hoặc c= 0 hoặc d = 0 thì bất đẳng thức luôn đúng. Vì thế chúng ta cũng chỉ chứng minh bất đẳng thức với 4 số dương mà thôi:

Bài tập ứng dụng

Các hệ quả của bất đẳng thức

Từ việc chứng minh bất đẳng thức Cosi ta có thể đưa ra một số khẳng định sau và áp dụng được vào chứng minh đại số. Những hệ quả này bao gồm:

• Tổng của một số thực dương và nghịch đảo của nó sẽ luôn có giá trị tối thiểu bằng 2,

(x+1x)min=2 x>0, R

• Tích của hai số thực dương có tổng không đổi đạt giá trị lớn nhất khi hai số đó bằng nhau
• Tổng của hai số thực dương có tích không đổi sẽ đạt giá trị nhỏ nhất khi 2 số đó bằng nhau

Xem thêm:

Bất đẳng thức cauchy-schwarz

Bất đẳng thức bernoulli

Bất đẳng thức am-gm