Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn Giải SGK Toán 10 trang 29 – Tập 1 sách Cánh diều

Giải Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn sách Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo, dễ dàng đối chiếu kết quả khi làm bài tập toán trang 29.

Giải SGK Toán 10 Bài 2 trang 29 tập 1 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Mỗi bài toán đều được giải thích cụ thể, chi tiết. Qua đó giúp các em củng cố, khắc sâu thêm kiến thức đã học trong chương trình chính khóa; có thể tự học, tự kiểm tra được kết quả học tập của bản thân.

Giải Toán 10 trang 29 Cánh diều – Tập 1

Bài 1 trang 29

Kiểm tra xem mỗi cặp số (x;y) đã cho có là nghiệm của hệ bất phương trình tương ứng không.

Gợi ý đáp án

a) Thay x = 0,y = 2 vào hệ 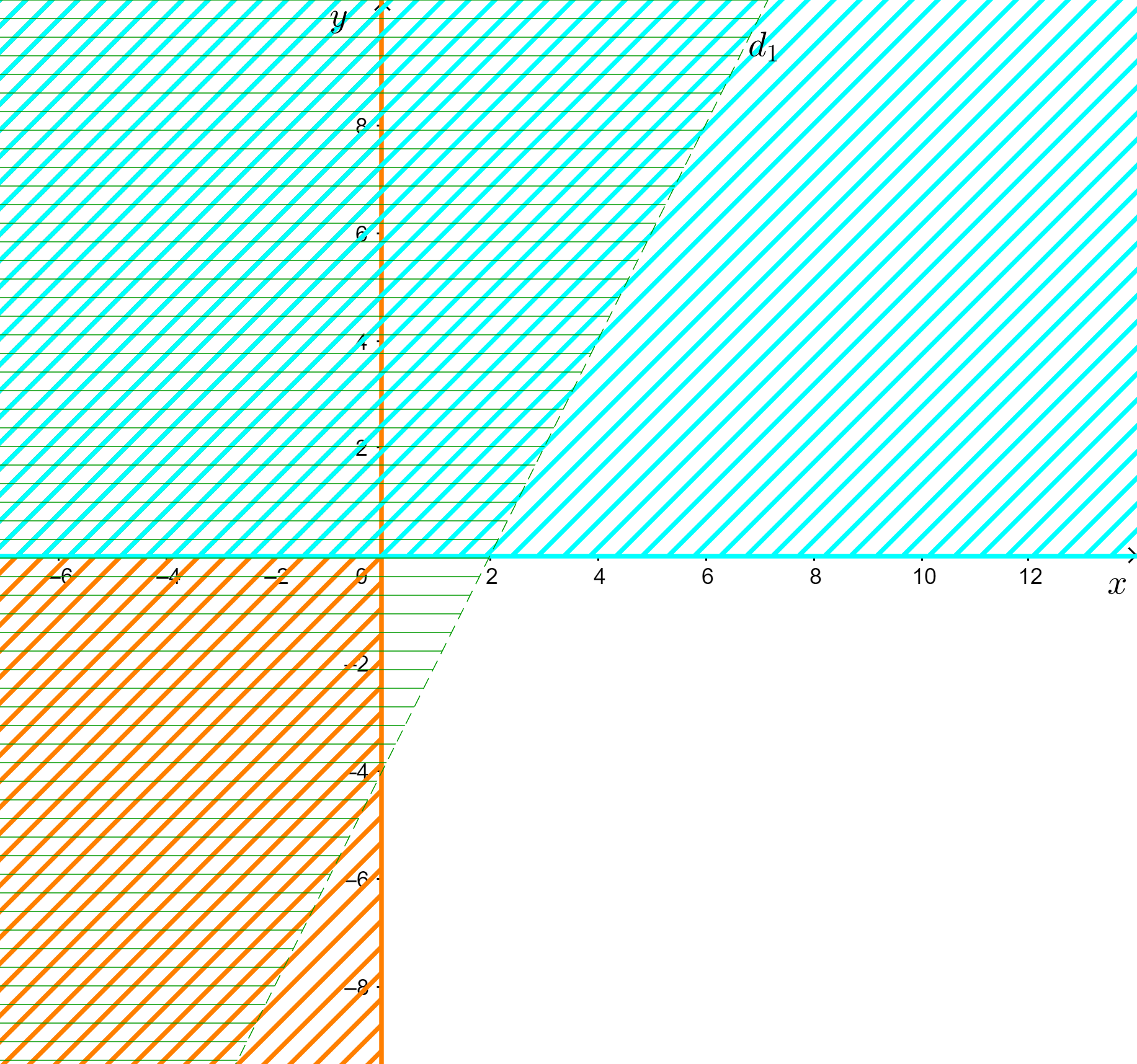ta được:

(Đúng)

Thay x = 1,y = 0 vào hệ ta được:

Vậy 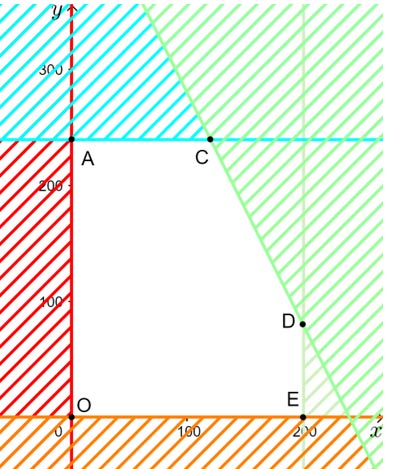là nghiệm của hệ còn không là nghiệm.

b) Thay x = – 1,y = – 3 vào hệ ta được:

(Đúng)

Thay x = 0,y = – 3 vào hệ ta được:

Vậy là nghiệm của hệ còn không là nghiệm.

Bài 2 trang 29

Biểu diễn miền nghiệm của hệ bất phương trình:

Gợi ý đáp án

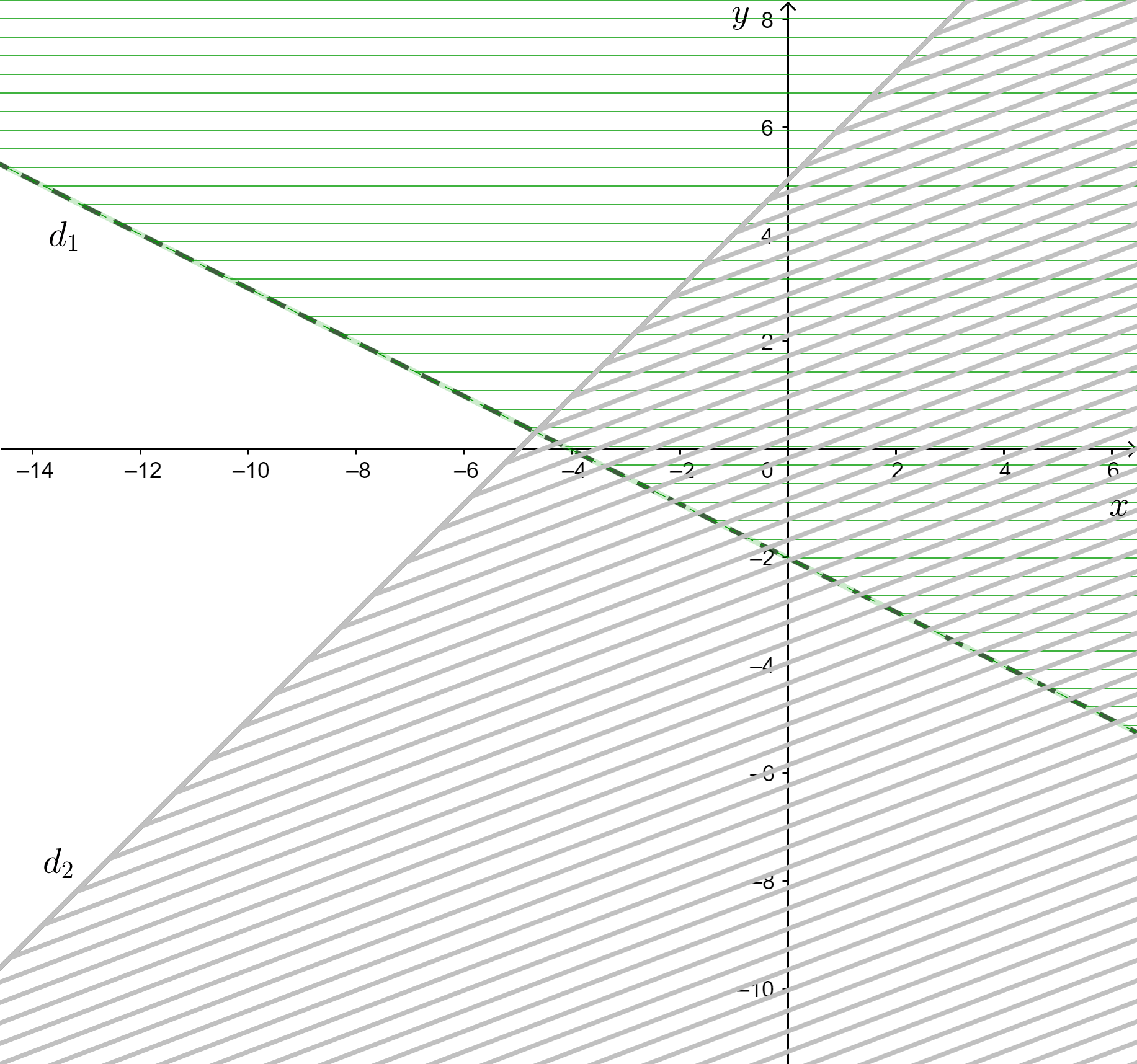
a) Vẽ các đường thẳng x + 2y = – 4(nét đứt) và y = x + 5 (nét liền)

Thay tọa độ O vào x + 2y < – 4 ta được: 0 + 2.0 < – 4 (Sai)

=> Gạch đi phần chứa O.

Thay tọa độ O vào ta được: (Sai)

=> Gạch đi phần chứa O.

Miền nghiệm của hệ:

Từ hình vẽ ta thấy hệ vô nghiệm.

b) Vẽ các đường thẳng 4x – 2y = 8 (nét đứt) và hai trục (nét liền)

Thay tọa độ O vào 4x – 2y > 8 ta được: 4.0 – 2.0 > 8 (Sai)

=> Gạch đi phần chứa O.

Với thì gạch phần bên trái Oy

Với thì gạch bên trên Ox

Miền nghiệm của hệ:

Bài 3 trang 29

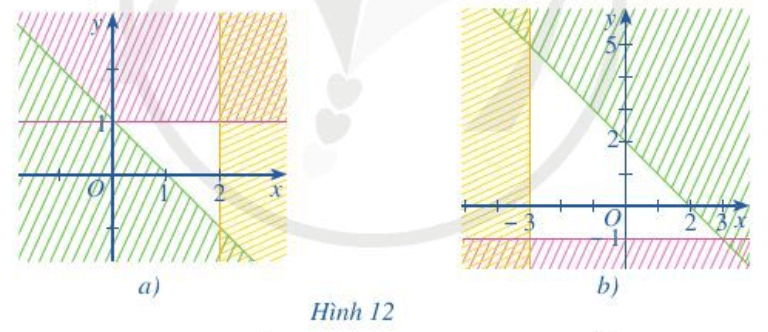
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

Gợi ý đáp án

Hình 12a

Ta thấy các đường thẳng trên hình là y = 1;x = 2;y = – x + 1

Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.

Hình 12b.

Ta thấy các đường thẳng trên hình là y = – 1;x = – 3;x + y = – 2

Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp

Bài 4 trang 29

Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.

Gợi ý đáp án

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là x và y . Biểu diễn các đại lượng khác theo x và y.

Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là x và

Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có

Thời gian làm y chiếc kiểu 2 trong một ngày là

Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai nên thời gian làm mũ thứ nhất là 1 giờ làm được 30 chiếc.

Thời gian làm x chiếc kiểu 1 trong một ngày là

Tổng thời gian làm trong một ngày là 8h nên ta có:

Bước 2: Lập hệ bất phương trình.

Bước 3: Biểu diễn miền nghiệm.

Miền biểu diễn miền nghiệm là phần màu vàng:

Bước 4: Tìm x và y để tiền lãi cao nhất.

Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm left( {x;y} right) là một trong các đỉnh của tam giác màu vàng:

T = 24x + 15y

(nghìn đồng)

(nghìn đồng)

Số lượng mũ kiểu 1 là 240 và số lượng mũ kiểu 2 là 0